students

PhD. and Post-doc Students I work(ed) with during the last years.

phd_arzhela.jpg

Arzhela ROPERCH (PhD started on November 2, 2024)

Reinforcement Learning fo Topological Optimization of Block-Structured Meshes

Supervision: F. Ledoux and J.-Ch. Janodet (AROBAS, IBISC, Université Evry, Paris-Saclay)

This PhD project aims to develop a learning method based on an actor-critic algorithm, i.e. a temporal difference algorithm using gradient descent, composed with the use of Monte Carlo Tree Search, or MCTS for Monte Carlo Tree Search. An actor-critic algorithm is based on two components: an actor who decides which action to choose for a given state; a critic who evaluates the action taken by the actor and will indicate how good the action taken is and how to adjust it. Based on recent results, in which the PPO algorithm is used to provide a solution to a problem of topological modification of 2D meshes, and on the use of MCTS, we wish to propose an approach to modify 3D block structures. As part of the thesis, the results obtained will be confronted with real industrial use with test cases significant to the needs of the CEA.

phd_tristan.jpg

Tristan CHENY (PhD started on October 21, 2024)

Anisotropic block-structured mesh generation for extern aerodynamics

Supervision: D. Sokolov (PIXEL, LORIA, Université de Lorraine), E. Corman (PIXEL, LORIA, CNRS) and F. Ledoux

The proposed PHD work is related to the Simulation program of the CEA DAM. Started in 1996, this program aims to ensure reliability of the French nuclear charges, without nuclear experiment. To this purpose, it relies on Numerical Simulation. Here, we focus on codes of the Simulation program that require to discretize studied objects under the form of a mesh. Many of these codes require quadrangular meshes (in 2D) or hexahedral meshes (in 3D) that are block-structured, with in addition a high control over the direction and size of the mesh elements. To our knowledge, the generation of this kind of meshes is mainly processed by hand, thanks to interactive softwares, which is expensive in engineer-time.

phd_isaie.jpg

Isaïe MURON (PhD started on January 22, 2024)

Efficient mesh algorithms on massively parallel architecture

Supervision: F. Ledoux and C. Chevalier (LIHPC, CEA)

High-fidelity simulation of complex phenomena is today an essential tool in many scientific fields. At CEA, we develop our own simulation software and environmental tools (meshing, visualization), capable of exploiting powerful computers equipped with hundreds of thousands of processors composed of heterogeneous calculation units ( CPU and GPU). To effectively operate such computers, it is necessary to specifically adapt the data structures and algorithms. In this thesis, we are interested in remeshing algorithms, which belong to the category of irregular problems, for which successive memory accesses affect non-contiguous areas, and this in an unpredictable manner. This characteristic makes efficient parallelization problematic on current and future processors. It is this problem that we wish to provide a solution to. More precisely, the objective of the thesis work is to define a data structure and a parallel programming paradigm for 3D remeshing within the gmds mesh library. Considering the case of simplicial and mixed meshes, the thesis work will consist of extending existing parallelization concepts to exploit any type of many-core architecture (including GPUs)

phd_paul.jpg

Paul BOURMAUD (PhD started on October 1st, 2022)

Monte-Carlo Tree Search for Hexahedral Blocking

Supervision: J.-Ch. Janodet (AROBAS, IBISC, Université Evry, Paris-Saclay) and F. Ledoux

Preparing high-fidelity simulations that requires block-structured hexahedral meshes is extremely time consuming : highly skilled engineers have to manually decompose CAD models into a set of hex-meshable structured blocks. This manual process, called the blocking stage, is a bottleneck for incremental design and sensitivity analysis: current approaches fail to propose an automatic solution to any 3D shapes. However, as engineers are able to create such meshes using interactive tools, we strongly believe that machine learning techniques are worth investigating.

The aim of the thesis is to participate to develop and test a Reinforcement Learning framework dedicated to decompose a CAD model into ready-to-use hex-meshable blocks. We mainly focus on the usage of Monte-Carlo Tree Search in this work.

phd_sebastien.png

Sébastien MESTRALLET (PhD from 10/2021 to 11/2024)

Robust polycubes for block-structured hexahedral mesh

Supervision: F. Ledoux and C. Bourcier (SGLS, Université Paris-Saclay, CEA)

PhD defended on November 28, 2024

In order to make computations on discrete models, hexahedral meshes are often needed because:

  • some computation codes can only manage hexahedral elements (or these codes are only qualified for hexahedral elements)
  • hexahedral elements allow to get a mesh with less number of elements in shapes with small thickness
  • hexahedral elements obtained by block splitting have in general good aspect ratio, allowing a better convergence and a better quality of the result of the simulation.

The current hexahedral meshing algorithms (using octree method or cartesian grid) do not always allow to have a mesh with a good enough quality to be usable as the input of a numerical simulation. Some cells are too distorted near curved faces and refinement areas. As a result, our colleagues often have to make a manual block splitting of the geometry in hexahedral blocks, which is tedious and takes a long human time (from several days to several months), and is sometimes impossible. Some new automatic methods like polycubes or field frames are being developed in the academic world but they are not robust enough to guarantee a good-quality mesh on every geometry. Hence, this is an open problem. The aim of this thesis is to find iterative/evolutionary algorithms that can be applied to robust and good quality hexahedral mesh generation.

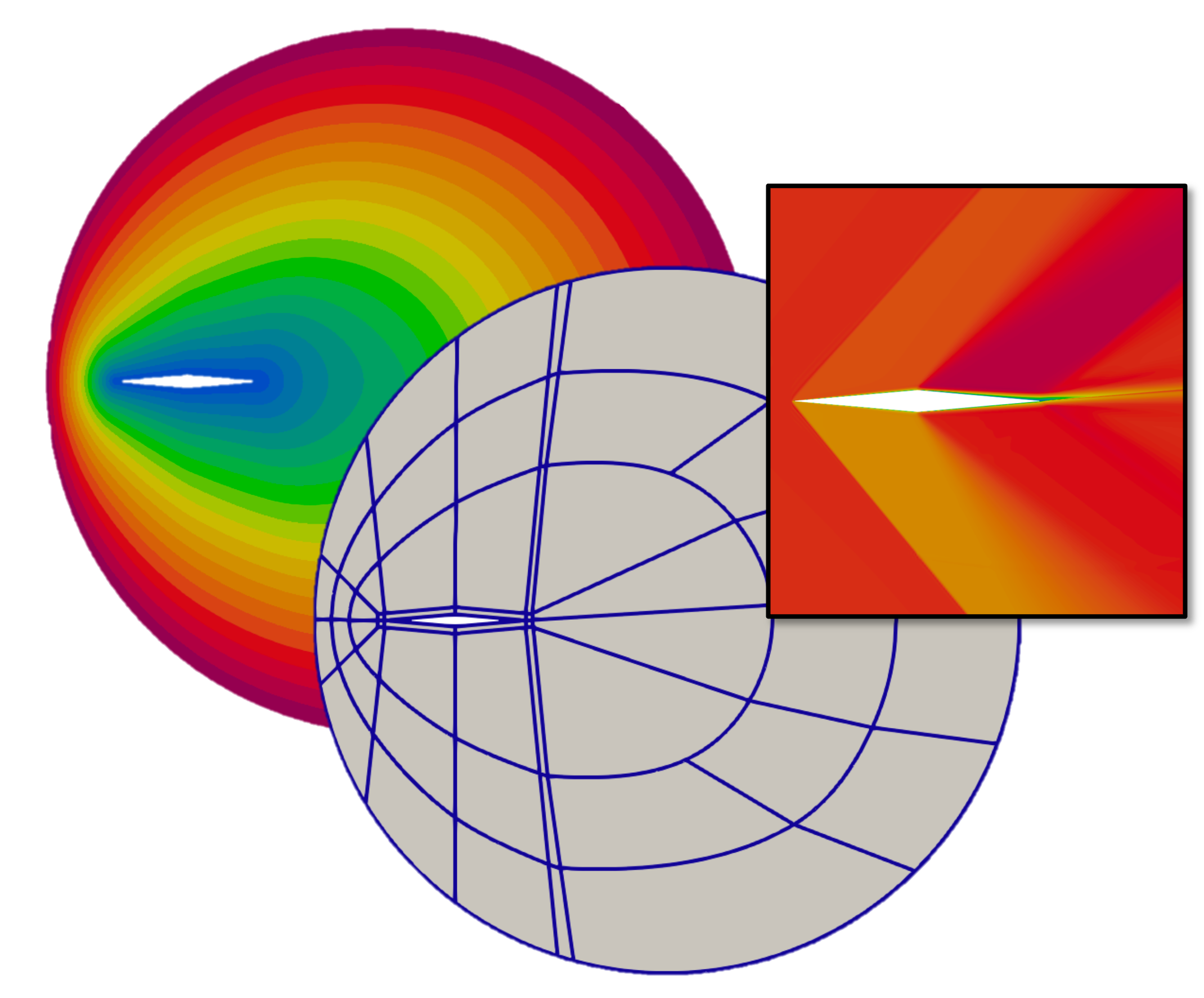
phd_claire.png

Claire ROCHE (PhD from 10/2021 to 10/2024)

Hexahedral curved block-structured mesh generation for atmospheric re-entry

Supervision: F. Ledoux, J. Breil (CEA, CESTA) and T. Hocquellet (CESTA, CEA)

PhD defended on October 1st, 2024

The French Alternative Energies and Atomic Energy Commission (CEA) studies Computational Fluid Dynamics (CFD) in the case of supersonic and hypersonic flows. To do so, a dedicated code is developed. To deal with strong constraints, this code only performs on block-structured meshes. This specific type of mesh is complicated to generate, and this generation is usually handled by hand using dedicated interactive software. In the case of industrial complex geometries, the mesh generation is highly time-consuming. Currently, automatic hexahedral mesh generation is a complex open research field.In this thesis work, we propose a method to generate block-structured hexahedral meshes on curved blocks of the fluid domain around vehicles, dedicated for the problems of interest. This method is first proposed in 2D and then extended to 3D. Here, it is presented in the generic nD case. This method is composed of several steps. First, a linear block structure is extruded from a first vehicle surface discretization. This work is an extension of the previous work of Ruiz-Girones et al.. Once this linear block structure is generated, we propose two different methods to curve the block structure to improve the vehicle surface representation and limit the smoothing on the final mesh. The first method is through an algorithm of mesh adaptation at fixed topology by solving an optimization problem to which a penalty term is added to align certain mesh edges to an implicit interface. Our global approach uses this method to align the block structure to the vehicle surface. This method remains time-consuming in 3D, so we proposed a second method to curve our block structure through polynomial Bézier curves. Considering our blocks as Bézier blocks, we apply geometric and local operations to align the high-order block structure to the vehicle surface. Then, considering we curved the block structure using Bézier elements, we generate a mesh on the curved blocks under constraints. Finally, the generated mesh quality is evaluated in two ways. The first one is through purely geometrical criteria analysis. The second one is through numerical simulations of flows around vehicles on our meshes, comparing the simulation results to experimental data, analytical results, and reference simulations.

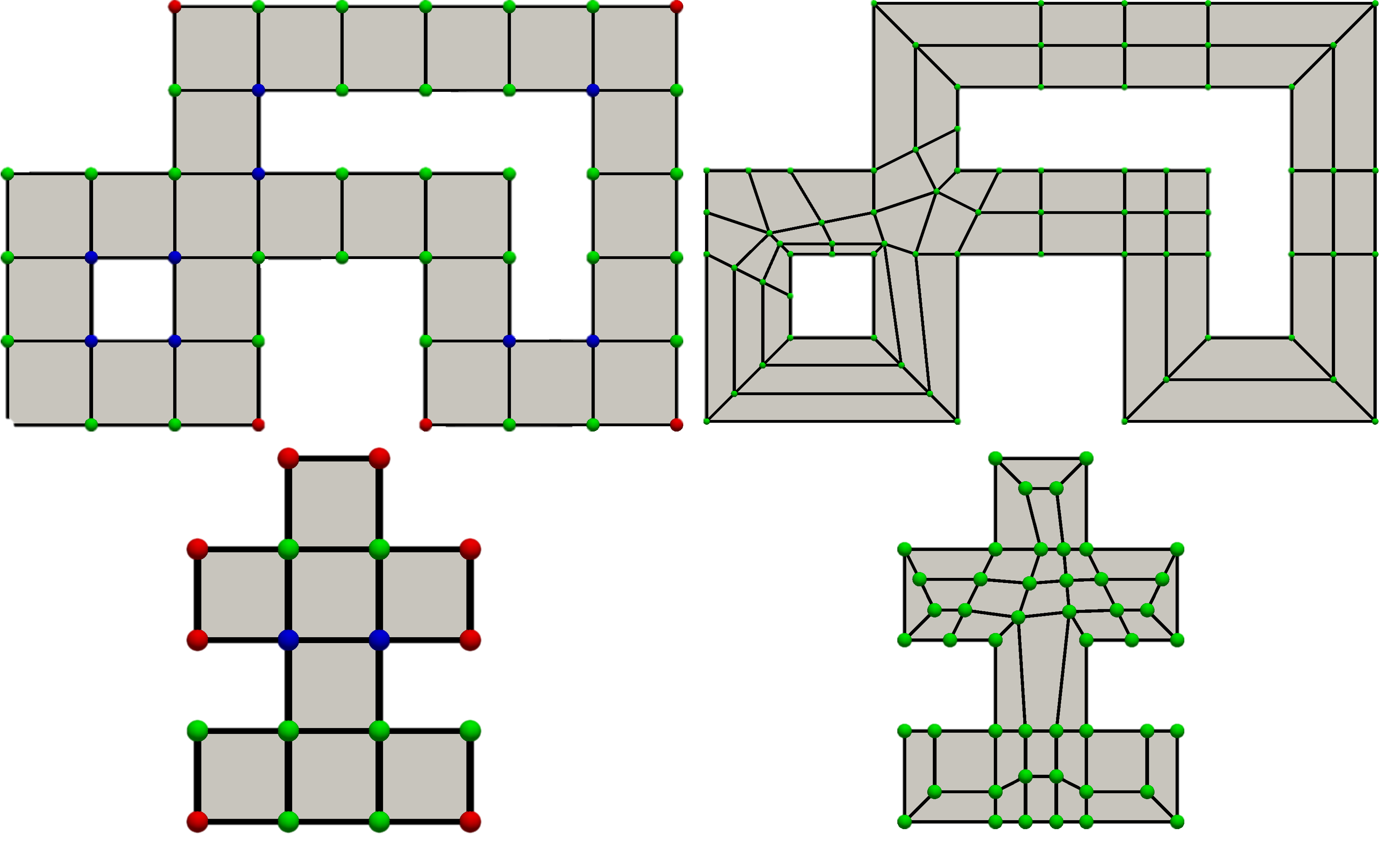
phd_valentin.png

Valentin POSTAT (PhD from 10/2020 to 01/2024)

Representation and optimization of block-structured meshes using multi-agent systems

Supervision: G. Hutzler (*COSMO, IBISC, Université Evry, Paris-Saclay) and F. Ledoux

PhD defended on January 24, 2024

This thesis deals with the representation and generation of block-structured hexahedral meshes. To date, there is no method for generating satisfactory block structures for any geometric domain. In practice, expert engineers generate these meshes using interactive software, which can take several weeks to complete. Moreover, adding modification operations in these interactive softwares is a delicate task to maintain the coherence of the block structure and its relationship with the geometric domain to be discretized. In order to improve this process, we first propose to define hexahedral mesh manipulation operations based on the use of the generalized map model. Then, by considering block structures obtained using the Polycube method, we provide methods for optimizing the topology of these structures to satisfy constraints of a geometric nature. We propose a first method in dimension 2, which considers a local approach to the problem based on the experience of engineers working with interactive software. We then propose a second method, this time using ant colony optimization meta-heuristics for leaf selection in dimension 3.

phd_hubert.png

Hubert HIRTZ (PhD from 12/2020 to 12/2023)

Mesh partitioning for load balancing multiphysics simulations

Supervision: F. Ledoux, C. Chevalier (LIHPC, CEA) and S. Morais (LIHPC, CEA)

PhD defended on December 12, 2023

This study aims to improve the performance of large-scale, distributed, mesh-based simulations. More specifically, we take an interest in improving the balance between the load on each computation unit on which the simulations execute. Load balancing mesh-based simulations generally involve both the load of each mesh cell and the data transfers between computation units. State-of-the-art tools most commonly solve this problem in one way, which is not always the most optimal for a given simulation, because their scope is broader than that of mesh partitioning and load-balancing. Our study aims to fill this gap and implement a new partitioning tool dedicated to meshes and load-balancing. After an in-depth presentation of the context and issues related to balancing the load of distributed, mesh-based simulations, as well as the definition of common mesh-partitioning-related problems and associated, state-of-the-art algorithms to solve each of these problems, we present a new method to partition meshes, which involves carefully chaining algorithms to optimise given mesh partition metrics. We then develop this method in two ways:

  • first, we expand the number partitioning algorithm called VNBest so that it can balance load against target weights.
  • Second, we adapt the geometric algorithm called RCB for cartesian meshes, to improve its performance on such meshes.

We implement the algorithm chaining method and its extensions in a new partitioning tool and describe its design thoroughly. We show our tool can compute partitions with better load-balance than state-of-the-art tools Scotch and Metis. However, the edgecut is not as optimised as in state-of-the-art. We present the scaling of our parallel implementation of partitioning algorithms.

phd_sofiane.png

Sofiane BENZAIT (PhD from 07/2020 to 09/2023)

Generation and Adaptation for hybrid meshes using oriented metrics

Supervision: F. Ledoux and A. Loseille (Gamma3, INRIA Paris-Saclay)

PhD defended on September 5, 2023

Today, fully tetrahedral mesh generation is a solved problem, but hexahedral mesh generation is not. The generation of hexahedral meshes is an important area of research in numerical simulation. Hexahedral meshes save time in numerical simulations compared with the same tetrahedral meshes. In addition to the possible time savings, hexahedral meshes can be used to study numerical solutions in certain imposed directions in a simpler way than with tetrahedral meshes. Given the difficulty of generating an entirely hexahedral mesh, one choice that can be made is to combine hexahedra and tetrahedra to generate mixed meshes. This solution makes it possible to have hexahedra in the areas of interest in the numerical simulation and tetrahedra in the rest of the mesh. The work in this thesis has led to the creation of a technique for generating mixed meshes using an orientation field and an imposed metric field as constraints. We chose a frontal approach for creating the vertices that form the mixed elements of the mesh and the cavity operator for modifying the initial tetrahedral mesh. Frontal generation is used to generate the curves, then the surfaces and finally the volume of the mesh. The generated vertices are then inserted into the initial mesh using the cavity operator, then the initial vertices of the mesh are removed using the cavity operator. The last step consists of reconstructing the hexahedra that could not be created by frontal generation by combining the tetrahedra to generate hexahedra. This last step is controlled by a pre-imposed quality factor.

phd_francois.png

François PROTAIS (PhD from 10/2019 to 10/2022)

Polycube-dominant meshing

Supervision: D. Sokolov (PIXEL, Université de Lorraine) and F. Ledoux

PhD defended on October 21, 2022

This thesis studies polycube methods for the generation of hexahedral meshes. These meshes, and more generally block structured meshes, are very much in demand for numerical simulations of physical phenomena (nuclear fission, flow, aerospace…). However, there is no industrially viable method to generate them. We are studying a family of methods that show great promise in filling this gap: global parametrization methods. To date, there are still many robustness problems, which we try to correct. For this purpose, we focus on the subfamily of polycube methods. To obtain a hexahedral mesh of a domain with polycubes - clusters of unit cubes -, the procedure is the following: the boundary of the domain is colored, then deformed according to these colors to have its boundary aligned with the axes, which makes it a extit{polycuboid}. This extit{polycuboid} is then intersected with a grid to give a polycube. Applying the inverse deformation on this polycube gives us a hexahedral mesh. We make two major contributions to this procedure: first, a method that allows to compute the deformation efficiently and with guarantees that it will be of good quality. Second, we introduce a new robust method to perform the grid intersection and deformation inversion steps. Finally, we present avenues of study for the difficult step of coloring, the last brick necessary to have robust methods for generating polycube-based hexahedral meshes.

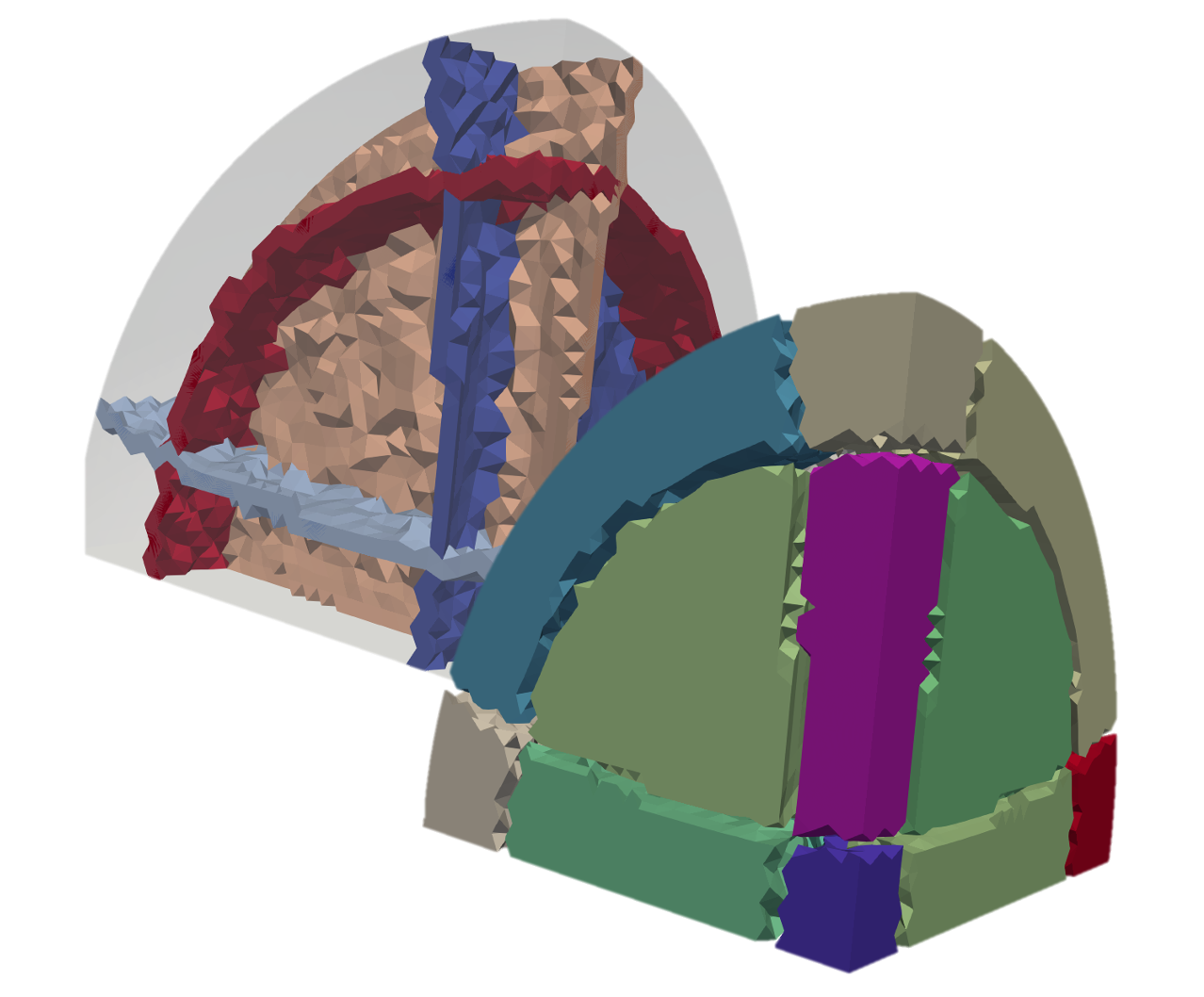
phd_simon.png

Simon CALDERAN (PhD from 10/2018 to 05/2022)

Interactive generation of block-structured hexahedral meshes

Supervision: G. Hutzler (COSMO, IBISC, Université Evry, Paris-Saclay) and F. Ledoux

PhD defended on May 17, 2022

The numerical simulation codes based on element and finite volume methods require discretizing the studied domain - for example a mechanical part such as a motor, an airplane wing, a turbine, etc. - using a mesh. In 3 dimensions, a mesh is a set composed of simple volumic elements, most often tetrahedrons or hexahedra, which partition the field of study. The choice of tetrahedrons or hexahedra is mainly dictated by the application (fluid-structure interaction, hydrodynamics, etc.). If the automatic generation of tetrahedral meshes is a relatively controlled process today, generating hexahedral meshes is still an open problem. This is problematic for applications that just imperatively require hexahedral meshes since their generation is done semi-automatically, which can take several weeks to several months of engineer time! While the time devoted to the digital simulation process itself tends to decrease due to the power of the machines used, the bottleneck is now in the preparation of the data, namely to obtain a CAD model adapted to the computation, then generate a mesh.It is in this context that we propose to develop a hybrid approach combining:1. The development of (semi) -automatic algorithms for generating and modifying block-structured hexahedral meshes;2. The implementation of an interactive graphic software dedicated to the manipulation of block structures. The interaction mechanisms will also be used to guide the algorithms in their decision-making, whether at initialization (criteria to be affixed to particular CAD entities) or in the course of an algorithm (decision between several options on which the algorithm cannot pronounce itself).The objective of this thesis is therefore not to provide a universal automatic solution, which seems unattainable at present, but rather to reduce the engineering time devoted to the generation of the mesh by providing more adapted tools. In this context, we propose to place the study as an extension of [LED10, KOW12, GAO15, GAO17], which considered the problem of simplification and enrichment of hexahedral meshes by insertion and removal of mesh layers. In all these works, the proposed algorithms are simple ‘greedy’ algorithms where the mesh is modified step by step to converge towards a final solution Ef: At each step Ei, one makes the hypothesis that the ‘best’ solution Ef will be obtained by making the ‘optimal’ choice for Ei. However, in operational research, such an approach is known to be perfectible since the problem of optimization treated is nonlinear. The idea is to use usual approaches in operational research and more specifically multi-agent systems, coupled to interactive tools, to allow the generation of block structures on complex CA0s

phd_nicolas_lg.png

Nicolas LE GOFF (PhD from 10/2018 to 12/2020)

Construction of a conformal hexahedral mesh from volume fractions : theory and applications

Supervision: J.-Ch. Janodet (AROBAS, IBISC, Université d’Evry, Paris-Saclay) and F. Ledoux

PhD defended on December 17, 2020

This thesis addresses the problem of the automatic generation of purely hexahedral meshes for simulation codes when having a mesh carrying volume fraction data as an input, meaning that there can be several materials inside one cell. The proposed approach should create an hexahedral mesh where each cell corresponds to a single material, and where interfaces between materials form smooth surfaces. From a theoretical standpoint, we aim at adapting and extending state-of-the-art techniques and we apply them on examples, some classically issued from CAD models (and imprinted onto a mesh to obtain volume fractions), some procedurally generated cases and others in an intercode capacity where we take the results of a first simulation code to be our inputs. We first define a metric that allows the evaluation of our (or others’) results and a method to improve those; we then introduce a discrete material interface reconstruction method inspired from the scientific visualization field and finally we present an algorithmic pipeline, called {sc ELG}, that offers a guarantee on the mesh quality by performing geometrical and topological mesh adaptation.

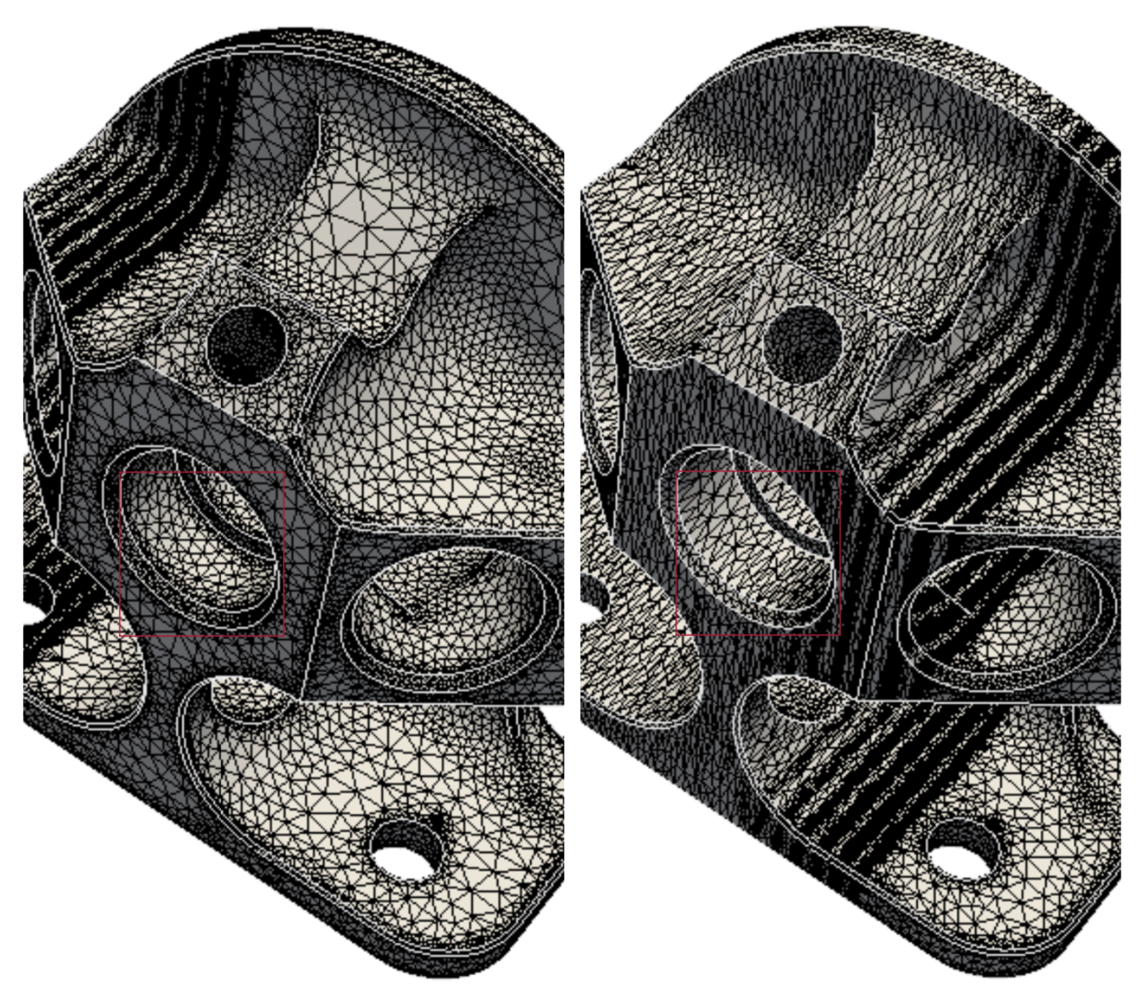
phd_hoby.png

Hoby RAKOTOARIVELO (PhD from 11/2014 to 07/2018)

A co-design approach of irregular kernels on manycore architectures : case of multi-scale anisotropic remeshing in computational fluid dynamics

Supervision: F. Pommereau (COSMO, IBISC, Université Evry, Paris-Saclay) and F. Ledoux

PhD defended on July 6, 2018

Numerical simulations of complex flows such as turbulence or shockwave propagation often require a huge computational time to achieve an industrial accuracy level. To speedup these simulations, two alternatives may be combined : mesh adaptation to reduce the number of required points on one hand, and parallel processing to absorb the computation workload on the other hand. However efficiently porting adaptive kernels on massively parallel architectures is far from being trivial. Indeed each task related to a local vicintiy need to be propagated, and it may induce new conflictual tasks though. Furthermore, these tasks are characterized by a low arithmetic intensity and a low reuse rate of already cached data. Besides, new kind of accelerators have arised in high performance computing landscape, involving a number of algorithmic constraints. In a context of electrical power consumption reduction, they are characterized by numerous underclocked cores and a deep hierarchy memory involving asymmetric expensive memory accesses. Therefore, kernels must expose a high degree of concurrency and high cached-data reuse rate to maintain an optimal core efficiency. The real issue is how to structure these data-driven and data-intensive kernels to match these constraints ?In this work, we provide an approach which conciliates both locality constraints and convergence in terms of mesh error and quality. More than a parallelization, it relies on redesign of kernels guided by hardware constraints while preserving accuracy. In fact, we devise a set of locality-aware kernels for anisotropic adaptation of triangulated differential manifold, as well as a lock-free and massively multithread parallelization of irregular kernels. Although being complementary, those axes come from distinct research themes mixing informatics and applied mathematics. Here, we aim to show that our devised schemes are as efficient as the state-of-the-art for both axes.

phd_sebastien_m.png

Sébastien MORAIS (PhD from 10/2013 to 11/2016)

Study and obtention of exact, and approximation, algorithms and heuristics for a mesh partitioning problem under memory constraints

Supervision: E. Angel (IBISC, Université Evry, Paris-Saclay),F. Ledoux and D. Regnault (IBISC, Université Evry, Paris-Saclay)

PhD defended on November 23, 2016

In many scientific areas, the size and the complexity of numerical simulations lead to make intensive use of massively parallel runs on High Performance Computing (HPC) architectures. Such computers consist in a set of processing units (PU) where memory is distributed. Distribution of simulation data is therefore crucial: it has to minimize the computation time of the simulation while ensuring that the data allocated to every PU can be locally stored in memory. For most of the numerical simulations, the physical and numerical data are based on a mesh. The computations are then performed at the cell level (for example within triangles and quadrilaterals in 2D, or within tetrahedrons and hexahedrons in 3D). More specifically, computing and memory cost can be associated to each cell. In our context, where the mathematical methods used are finite elements or finite volumes, the realization of the computations associated with a cell may require information carried by neighboring cells. The standard implementation relies to locally store useful data of this neighborhood on the PU, even if cells of this neighborhood are not locally computed. Such non computed but stored cells are called ghost cells, and can have a significant impact on the memory consumption of a PU. The problem to solve is thus not only to partition a mesh on several parts by affecting each cell to one and only one part while minimizing the computational load assigned to each part. It is also necessary to keep into account that the memory load of both the cells where the computations are performed and their neighbors has to fit into PU memory. This leads to partition the computations while the mesh is distributed with overlaps. Explicitly taking these data overlaps into account is the problem that we propose to study.

phd_nicolas_k.png

Nicolas KOWALSKI (PhD from 10/2010 to 10/2013)

Domain partitioning using frame fields: applications to quadrilateral and hexahedral meshing

Supervision: P. Frey (LJLL, Université Paris 6) and F. Ledoux

PhD defended on October 21, 2013

In this work, we describe a method to partition domains adapted to the generation of quadrilateral and hexahedral meshes. Given a domain D, the proposed approach proceeds in two steps: first, a frame field is defined on a background simplicial mesh of D. Then, singular elements of this field are extracted to create a skeleton that partitions D. The key element of this approach is the use of frames: at a point P of D, a frame allows to orient the quadrilateral or the hexahedral. Thus, we propose a complete study of frames and frame fields. We describe the proposed method both in dimension two and three. The main difference between the two is in the way frame fields are generated. In dimension 2, we solve a non-linear PDE, while in 2D, a heuristic is applied that uses initiallu an advancing front algorithm that takes the stability of the field into account, before using a smoothing algorithm. In both cases, a skeleton is extracted from the frame field. In dimension two, this skeleton always leads to a partition of D into quadrilateral-shaped blocks, and singularities are all of degree three and five. In dimension three, the obtained frame field leads to a partition allowing for hexahedral meshing in numerous cases. Many examples are showcased and compared to results obtained by existing methods.